[新しいコレクション] 円 接線 角度 341107-Autocad 円 接線 角度
円の位置関係と共通接線の本数の関係 2つの円が共通接線をもつ とき、共通接線はそれぞれの円と1点(接点)で交わります。 どちらの円にも同時に接している のが共通接線です。 この共通接線の本数は、2円の位置関係によって異なります。Jw_cadの作図(2)の〔 接線 〕は図面作成画面内描かれた円と円を繋ぐときや点と円を繋ぐときに使うコマンドですが、「角度指定」を使えば指定角度で円に接する線を描くことができます。 〔接線〕角度指定の使い方 〔 接線 〕コマンドを実行し、コントロールバーの「角度指定」のラジオである。 → a c = 180°, b d = 180°
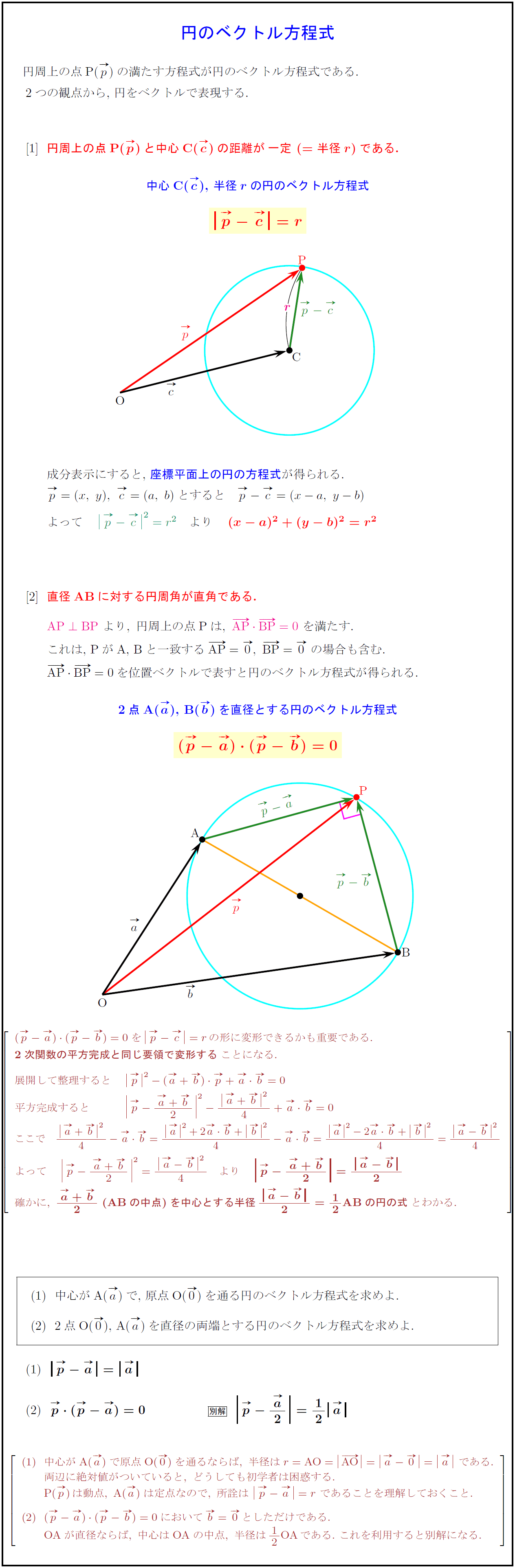
高校数学b 円のベクトル方程式2パターン 受験の月
Autocad 円 接線 角度
Autocad 円 接線 角度-「shift右クリック」で「接線」を選択します。 円をクリックします。 「@」を入力します。 長さ「100」を入力します。 「<」を入力します。 角度「1」を入力し、「Enter」します。 円に接していて角度が固定された線が作成されました。下図のように、中心oを通る直線と円との交点をdとします。 円に内接する四角形の対角の和は180°なので ・・・① となります。また1で証明した接弦定理を使うと ・・・② となり、直進の角度は180°なので ・・・③ となります。①、②、③を足せば



図形プログラミングの基礎 マウスでcanvas上の円弧をクリック検出 Satoh
「 円周角の定理の逆 」から POINT: 2 つの接点は、 A O を直径とする円周上にある。 直角三角形の合同条件「 斜辺と他の一辺がそれぞれ等しい 」より、上下 2 つの三角形は合同なので、 POINT:外部にある点 (A)から、ひいた 2 本の接線の長さは等しい楕円の接線の方程式 楕円 x2 a2 y2 b2 =1 x 2 a 2 y 2 b 2 = 1 の周上の点P (x0,y0) ( x 0, y 0) における 接線の方程式 は, である.円の接線とその接点を通る弦とがなす角は、その角内にある孤に対する円周角に等しい ※ ・接弦定理の証明(円周角が鋭角ver) ※ ・接弦定理の証明(円周角が直角ver)
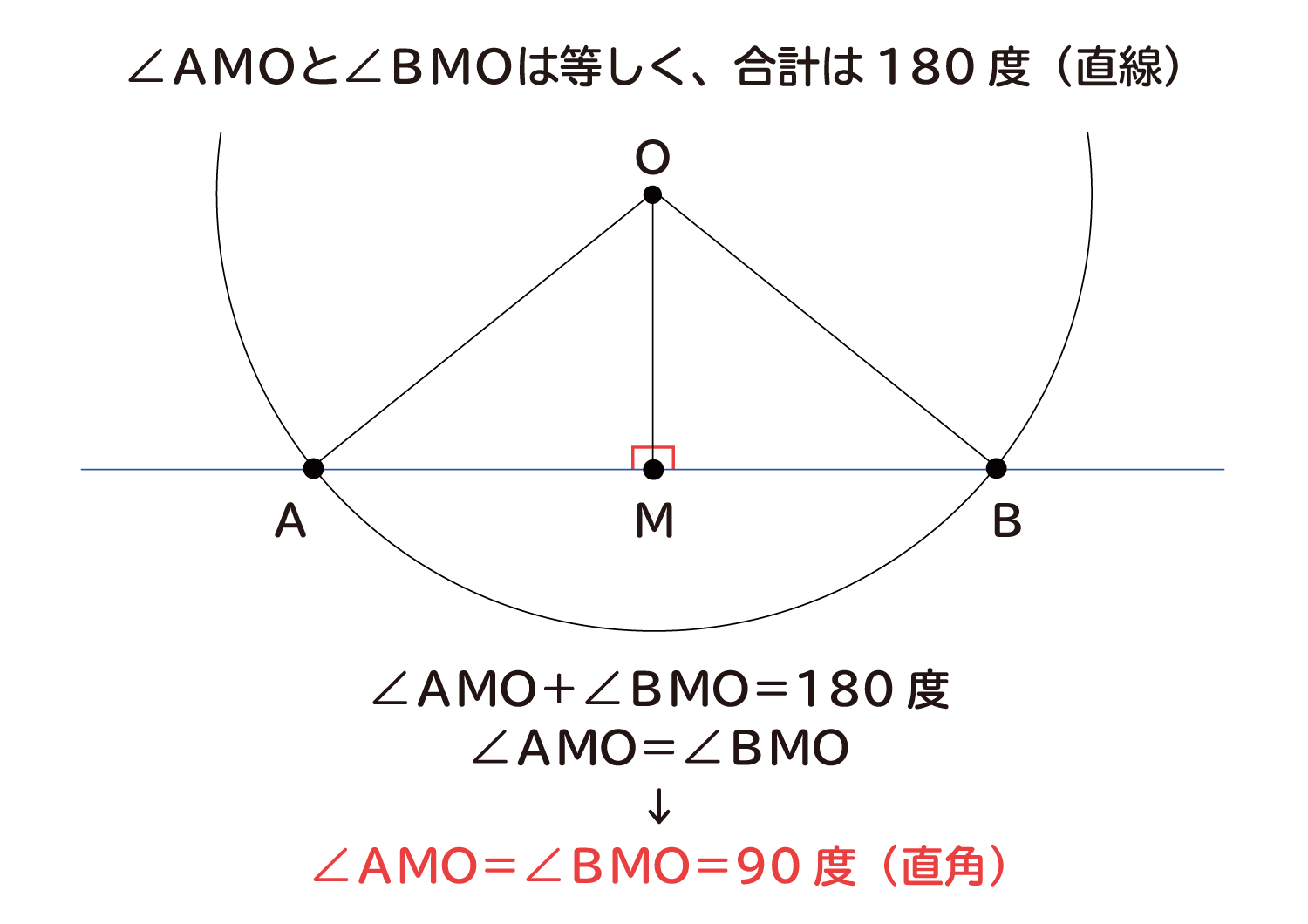
「円の接線は、接点を通る半径に垂直」になる説明 まずは、下の図のように円と2点で交わる直線を引いて、円と直線の交点を点A、点Bとします。 円の中心を点O、 直線ABの中点を点M とします。 ここで、三角形AMOと三角形BMOは、3辺の長さが全て同じなので、合同な三角形になっています。また、接線の傾きは、円の中心と接線を結んだ線と接線とが垂直に交わることから求めることができます。 接点が x 軸・ y 軸上にない場合、円の中心と接点を結んだ線の傾きは $\dfrac{y_1}{x_1}$ なので、接線の傾きは\ \frac{x_1}{y_1} \となります(参考: 基本垂直な直線接線の方程式を利用する 任意の点を通る円の接線を求めてみます。 まずは、原点中心とした半径 の円と、点p を考えましょう。 この円周上の任意の点a を通る接線は「円の接線を求める」で求めたように です。この直線が点pを通ることから が得られます。
角運動する物体の並進速度(接線速度)の求め方 角度を表す単位として、 rad(ラジアン) というものがあります。 これは端的に表すと、円の半径分の角度です。1radは下図の角度になります。 物理では、便宜上このradという単位で角度を記述することが多いの円の接線を角度をして描く方法をご紹介します。動画によるご説明もご参考にしてください。 操作手順 「作図」メニューより、「線」「角度線」を選択します。 接線を描く円を指定します。 角度を入力し「Enter」を押します。円の接線の方程式を求める公式の3通りの証明 レベル ★ 入試対策 座標,ベクトル 更新日時 座標平面において,円: x 2 y 2 = r 2 x^2y^2=r^2 x2 y2 = r2 上の点




円周角 三角形の外角の関係を使う問題



接弦定理とは 証明や定理の逆 問題の解き方 受験辞典
エクセルの関数は =ATAN2(xcxp, ycyp) となる。 P点、接点S1、円中心の角度は直角である。 よって、円中心、P点、接点S1の角度θは簡単に求まる。しかし接線は 線分コマンドでも作図することができるんです! 例えば、離れた箇所に円が2つ作図されているとします。 その円を接線で繋げてみましょう。 接線サーチを利用することで、接線系のコマンドを取り直すことなく、スムーズに作図が行え円の接線作図~基本~ 点Aを通るような円の接線を作図しなさい。 まずは円の中心と接点となる点Aを線で結びましょう。 すこしはみ出すように長めに書いてくださいね。 そして、この線に対して点Aを通るような垂線を引いていきます。 点Aにコンパスの針をおいて、適当な長さで円をかきましょう。 その円がぶつかった2点から、同じ半径を持つ円を2つかきます




接弦定理 5分で分かる3つの証明と分かりやすい解説 Rikeinvest




Wo14 号 プロペラファン プロペラファンを備えた送風機 プロペラファンを備えた空気調和機 プロペラファンを備えた室外機 および プロペラファンを備えた給湯器用室外機 Astamuse
円の接線の方程式 原点を中心とする半径 a a の円周上の点P (x0,y0) ( x 0, y 0) における接線の方程式は, x0xy0y= a2 x 0 x y 0 y = a 2 である.2円の交点を通る円の方程式 → 携帯版は別頁 原点を中心とする円の接線の方程式 円 x2y2=r2 の円周上の点 ( p , q) における接線の方程式は p x q y=r2 (1) 例1 ___円 x2y2=25 の円周上の点 (3 , 4) における接線の方程式は3x4y=25接線と半径は垂直 半径(正しくは円の中心と接点を結んだ線分)と、その点における接線は垂直 例題1 半径が \(11cm\) の円 \(O\) で、中心との距離が \(5cm\) である弦 \(AB\) の長さを求めなさい。 解答 このように、図が与えられないで出題されることもあり



内接円とは 内接円の半径の公式や求め方 性質 書き方 受験辞典
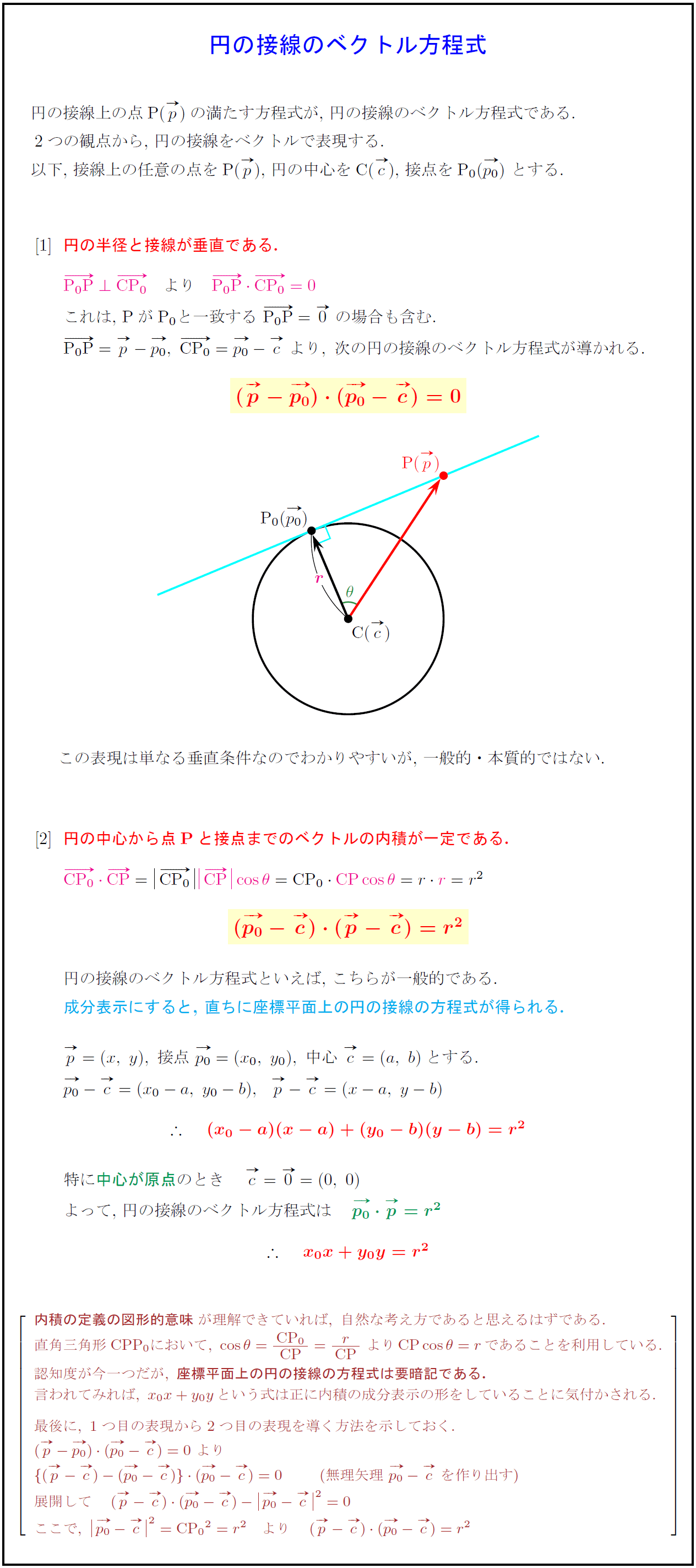



高校数学b 円の接線のベクトル方程式2パターン 受験の月
円運動する物体は円の接線方向に向かって動いている.速さvは(8112)式より,v=rωで一定となる.物体の位置が時間 とともに変化しているので,その時々の接線方向も違ってくる.したがって,速度の向きも時間とともに変化する. θ →r( 0) x y →r(t) O →v(02接線は、交点P(xp,yp)をとうり、角度(θα)と角度(θα)の線となる。 エクセルを用い円1と円2の共通接線を求める 円1の半径 R= 25 , 中心(xc1,yc1) = ( 05, 2) とする。円と接線に関する3定理(垂直、接線の長さ、接弦定理) 円の接線は,\ 接点を通る半径と垂直をなす 円の外部の点から引いた2本の接線の長さは等しい 接点を通る弦と接線が作る角は,\ その角内の弧に対する円周角に等しい (接弦定理) 方べきの定理接弦定理と内接四角形の関係 円とその接線が絡む構図を見かけたときはこの4つの定理の利用を想定しよう




円の接線 角度 エクセル関数 の出し方 W 550 H 1000の図形が Okwave
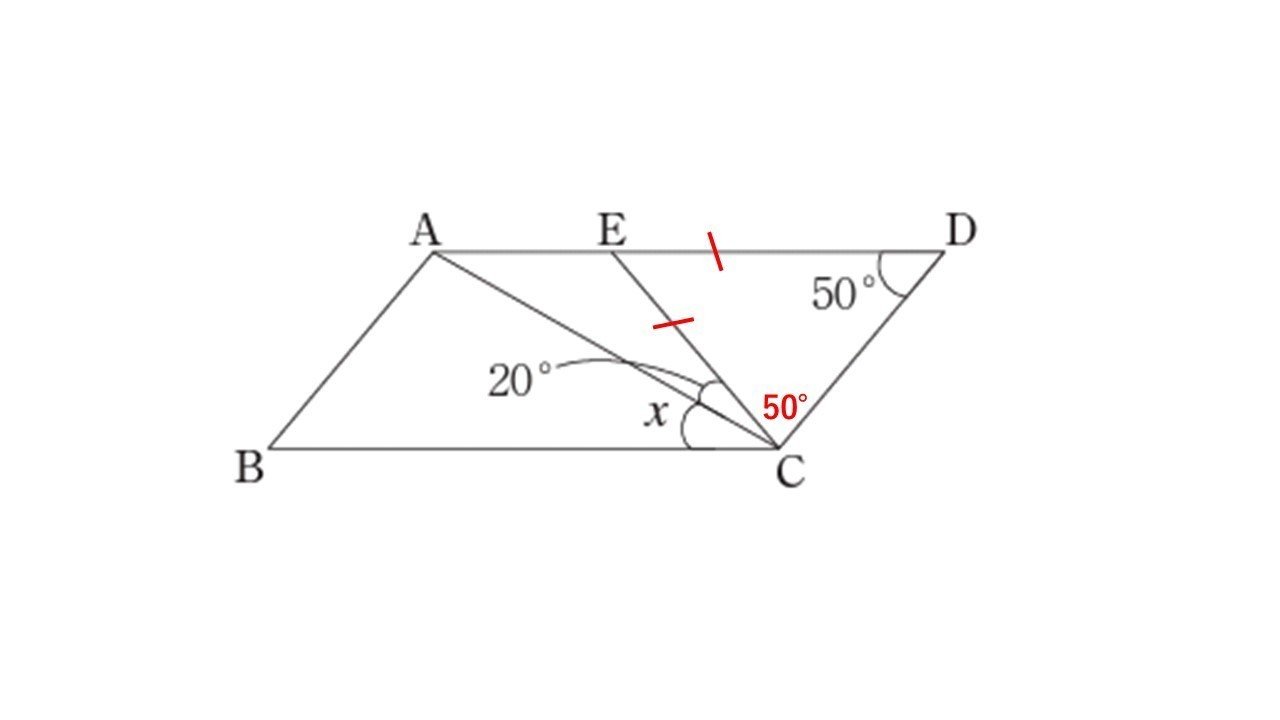



中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学と英語 Note
1004極線の方程式 円 と円外の点 について、点 から円には2つの接線が引ける。 その接線の接点をそれぞれ としたときの直線 の方程式を求める。 この直線 を円の 極線 、点 のことを円の 極 という。 点 の座標を 、点 の座標を をしたとき、 点 を通る円の2つの円の接線を作図する方法を以下に示します。 二つの円と距離を定義 2つの円の半径をr、r'中心間の距離をlと定義します。 r o r o' l 接線との平行線を作図 半径rの円と同心円の半径rrの円を作図します。 二つの円の中心を直径(oo')とする円を作図します。07このように 「円の中心と接点を結んだ線分」 と 「接線」 は 必ず垂直 になります。これは幾何学の範囲で学んだことです。 ということは、このように考えるのはいかがでしょうか。 接線の方程式は、円の中心と接点を通る直線と垂直に交わる と。
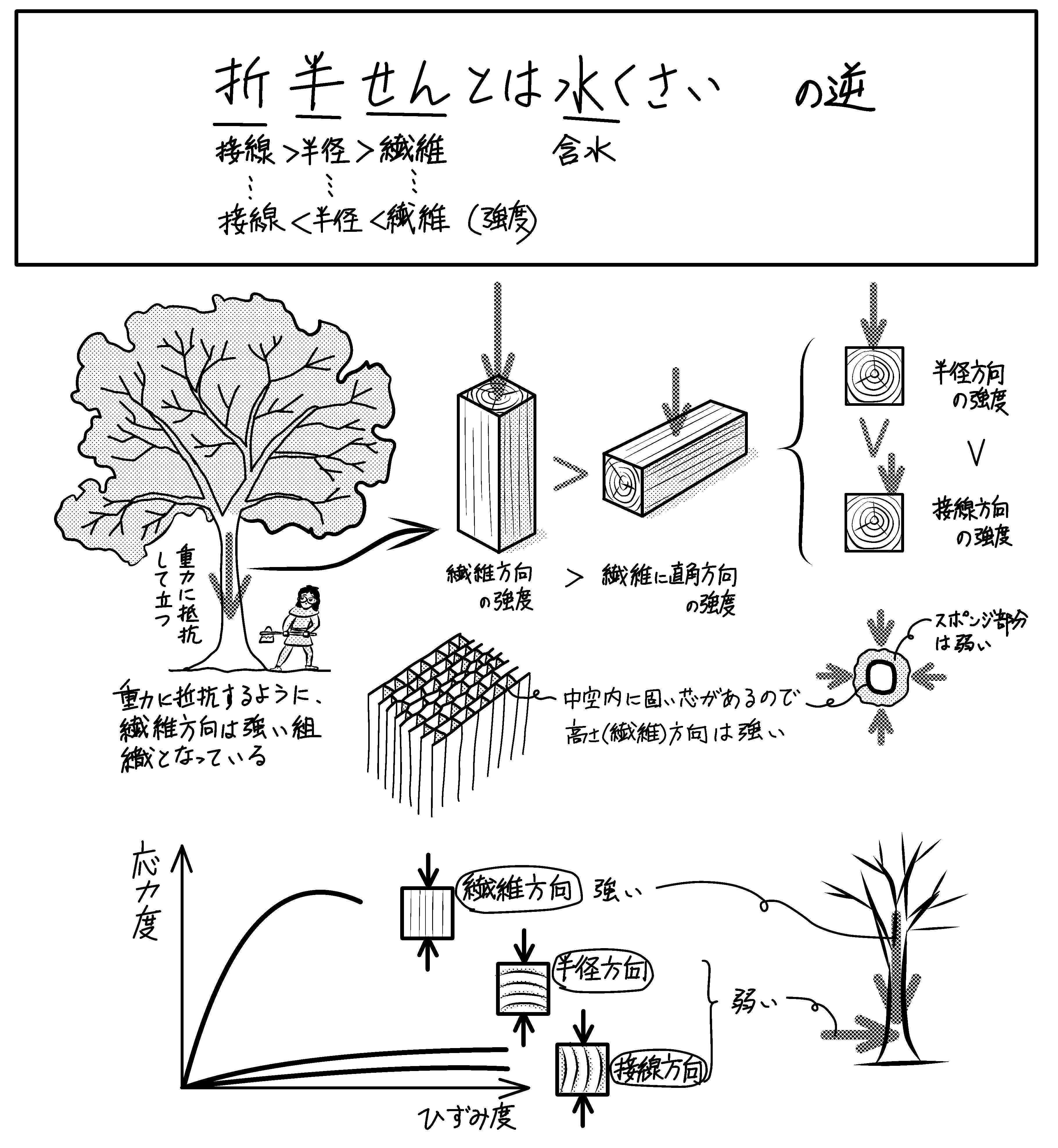



木材繊維の方向と強度の関係 記憶術あり ミカオ建築館 日記 楽天ブログ




高校数学b 円のベクトル方程式2パターン 受験の月
コントロールバー 点→円を選択する。 点を指示する (左クリック (L)で任意点、右クリック (R)で読取点)。円の接線の式の証明 上の公式の (1) の場合を証明してみましょう.(2) の公式は (1) の場合を平行移動すれば示すことができ円の接線とその接点を通る弦のつくる角は、その角の内部にある弧に対する円周角に等しくなる。 うーん説明だけを見ても 何を言っているのかサッパリ分かりませんね (^^;) 図を見ながらイチから解説していきますね。 まずは、円と接線があったとき 次に、接点を通る弦を引いてみます。 このとき、接線と弦のなす角ができますね。 この角を含む弧に対する




円の方程式と直線が切り取る弦の長さをわかりやすく解説




接弦定理とは 証明から覚え方まで早稲田生が徹底解説 高校生向け受験応援メディア 受験のミカタ
「円の接線 \(at\) と弦 \(ab\) が作る角 \(∠bat\) は、弦 \(ab\) に対する円周角 \(∠acb\) と等しい」という定理を、接弦定理と言います。 接弦定理は、\(∠BAT\) が鋭角・直角・鈍角のどの場合でも成り立ちますが、それぞれ証明の仕方が少しずつ変わってきます。円に内接する四角形の外角は,対角 (内角)に等しい。 → a の外角は c の角度と同じ。 証明 ここでは,a c = 180 を説明 (証明)します。 円 周 角 : に 対傍接円、傍心について 中学生へ 三角形の外角の二等分線の交点を「傍心ほ(ぼ)うしん」といい、傍心は全部で3つあり、下の図で ABCの傍心は点P、Q、R の3つです。 1990年ごろの中学の教科書にも傍心という用語は出てきませんが、傍接円と接線の長さ
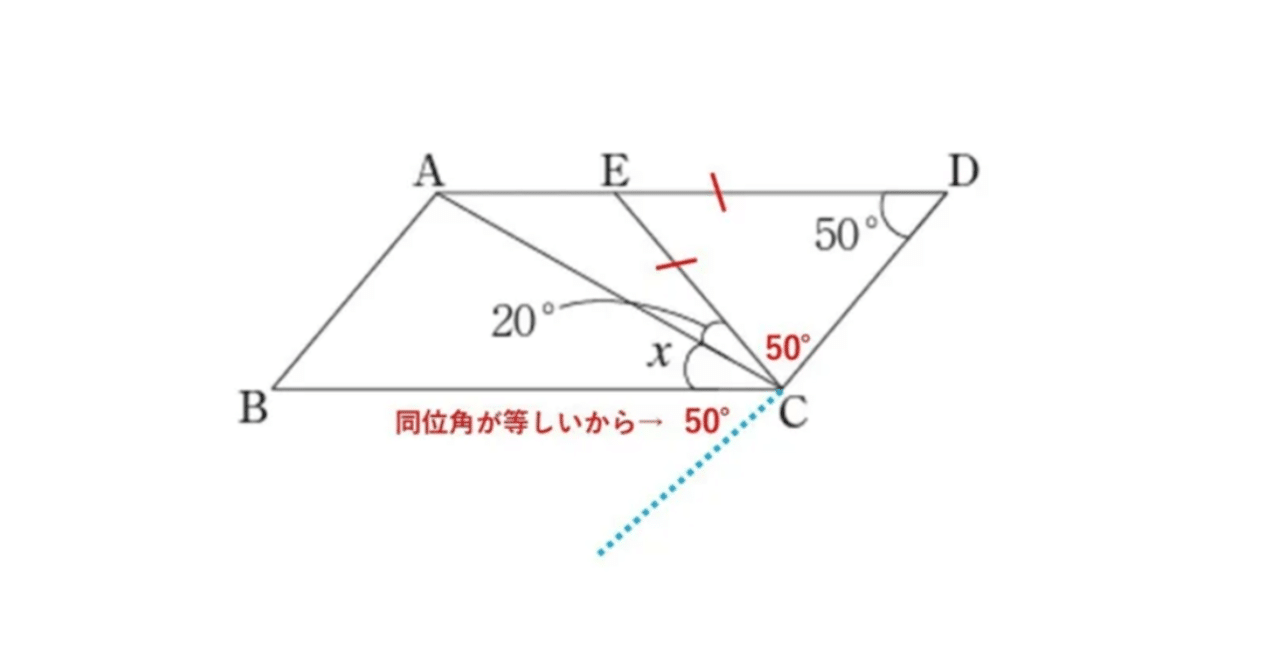



中学数学の平面図形の角度を求める問題を通して学び直しする論理 数学の基礎 タロウ岩井の数学と英語 Note




円の方程式と直線が切り取る弦の長さをわかりやすく解説
11 円の接線との関係 我々の接線の定義と現行のカリキュラムの整合 性を示すすなわち新しい定義によって引いた円 の接線が従来の定義と一致することを示す必要が ある 命頗1円()の円周上に点aをとる点j4を通 る円()の従来の意味の接線xax′を引く,次に円の接線と弦の作る角が(1)直角(90),(2)鋭角(90 より小さい),(3)鈍角(90 より大きい)の3つの場合に分けて示すこととします. (1) BAT=90 のとき (漢字2文字を入れなさい↓) 弦ABは になるので, (数字を入れなさい↓) BCA=無料アプリ(0円) 機能:交点・接点の座標や接円の中心座標などを求めることができます。 OS:PC用 (Windows8, 7, Vista, XP) 料金:無料 ダウンロード:下記画像をクリック(CAMESTホームページより) 機能:穴あけの中心XY座標を求めることができます。 OS



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル



パースのかかった円の描き方 デジタル限定 Remi S Essay
接弦定理:円の接線と弦の作る角 円の接線とその接点を通る弦とがなす角は、その角内にある孤に対する円周角に等しい このテキストでは、この定理を証明します。 円周角が鈍角の場合の証明 次の図のように円Oに接線をひき、その交点をAとする。実際にNCプログラムで使用することは少ないかもしれませんが、汎用性の高いマクロを作成するときに重要になる「円と2つの接線の角度や長さを求める方法」を紹介したいと思います。 上の画像のように、まず点 O を中心とする円を描き、その円の外側に点 A を置きます。 点 A を通る円との接線を2本引き、その接点を点 B、点 C とします。 2つの接点と点 O を結ふ三角比において、「単位円」は強力なツールです。 今回は tan \theta と単位円について、簡単なまとめです。 角度 \theta は反時計回りに増えます。 「単位円の接線 となるグラフ x=1 」と「角度 \theta と原点を結ぶ直線」とが ぶつかる点のy座標が、当該角度の tan \theta の値となります。
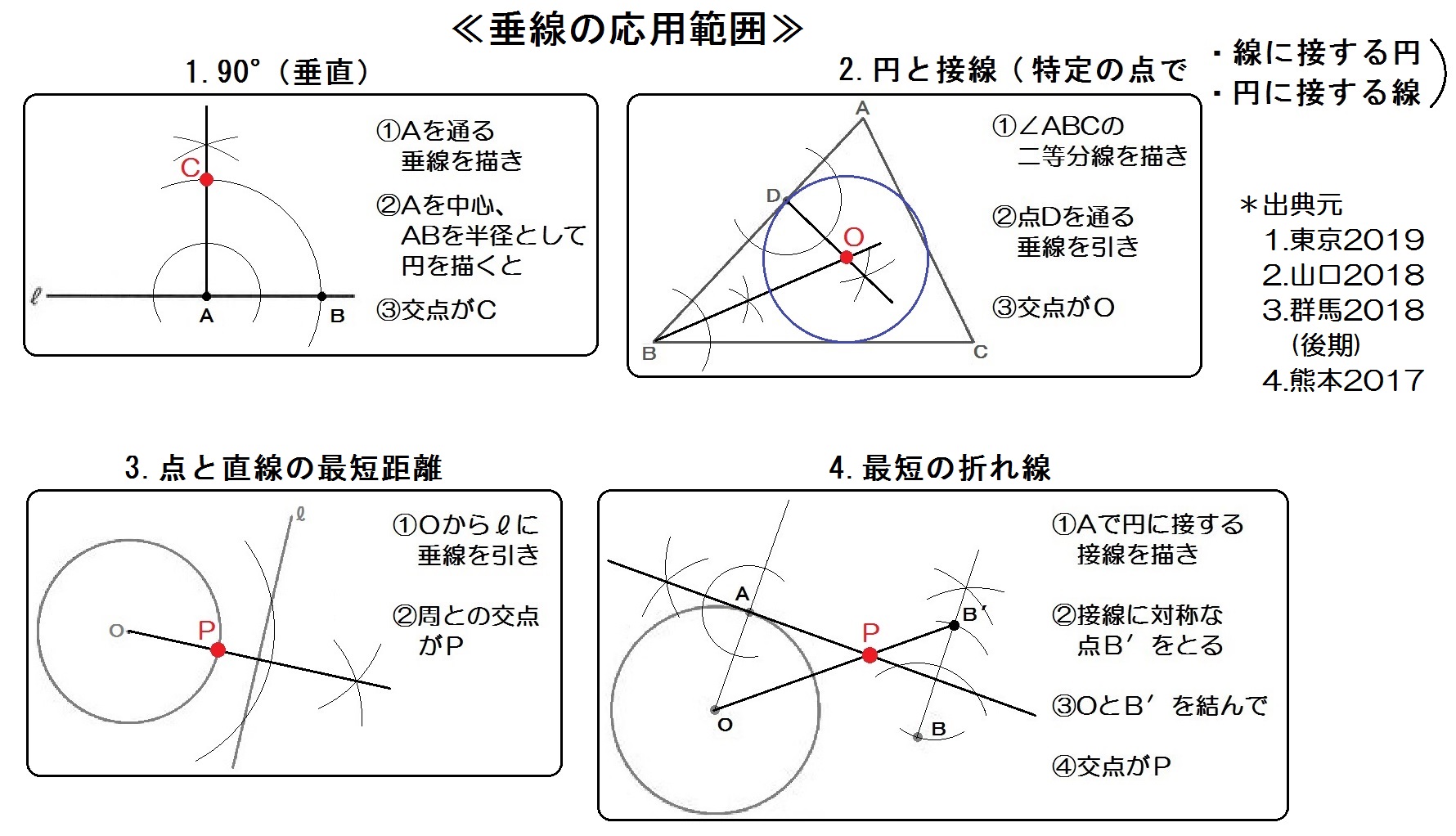



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図




数学 角度 の問題です 以下の二問について どうしても答えの出し方がわか Okwave
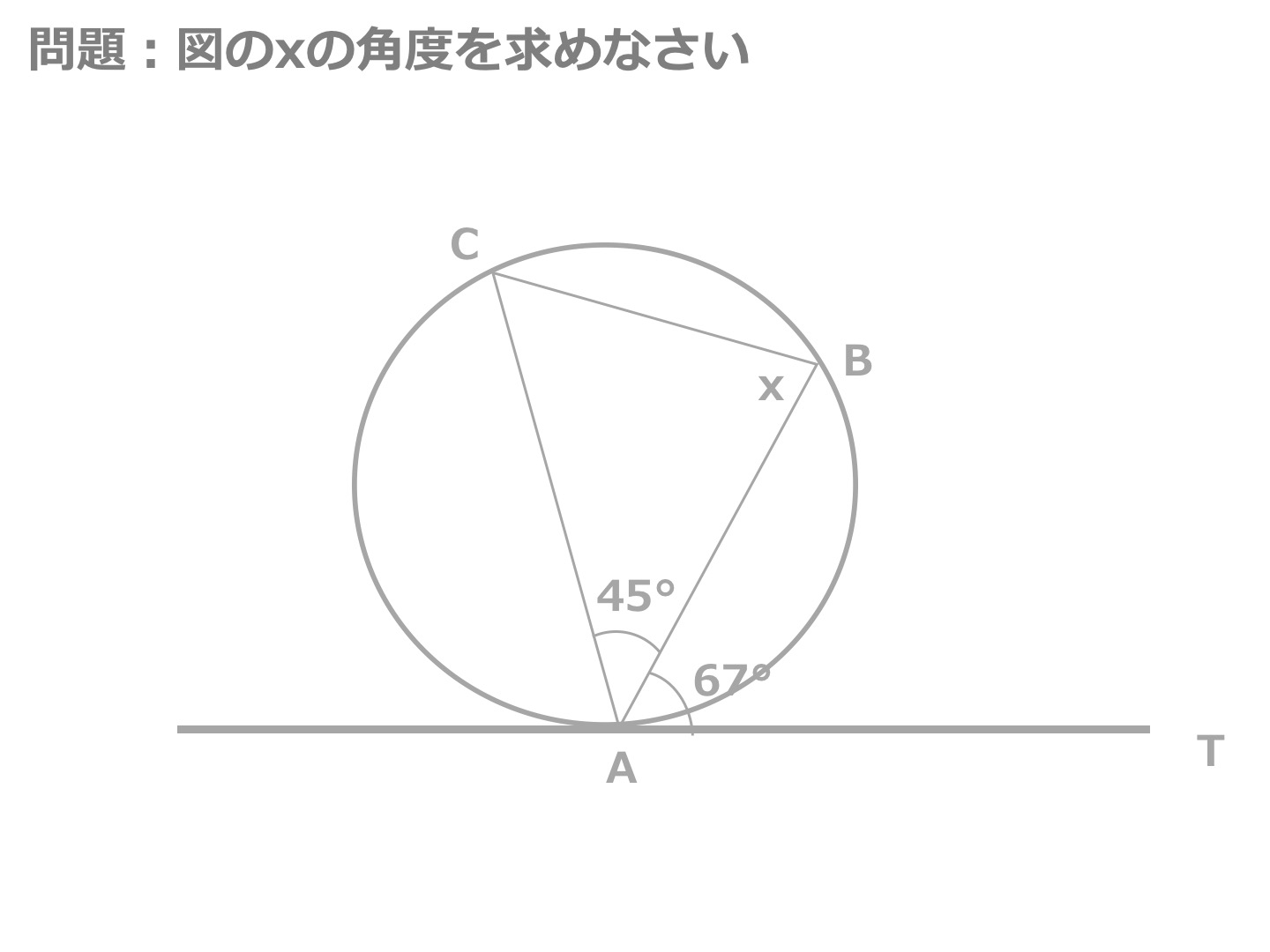
円の接線と角度 円の接線によってできる角度の問題を解いてみましょう。 はじめに、基礎知識を確認します。 円に接線を引くと、接点で半径と垂直に交わる。 1. 図1で、点Aと点Bは接点です。 ∠ x の大きさを求めてください。 (島根県高) 2.
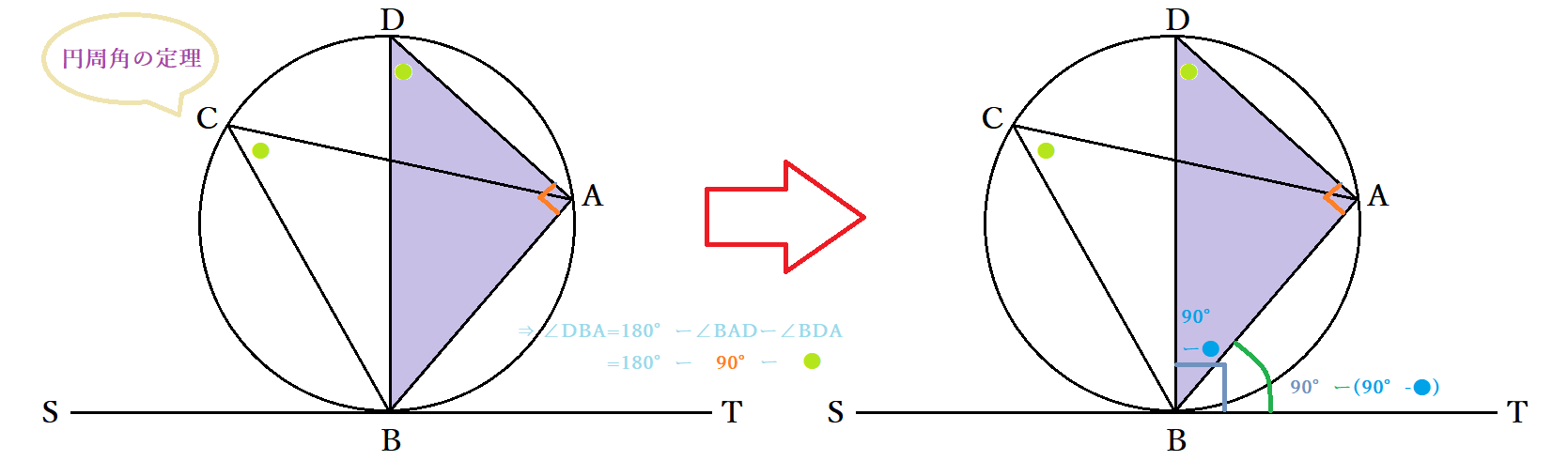



接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog
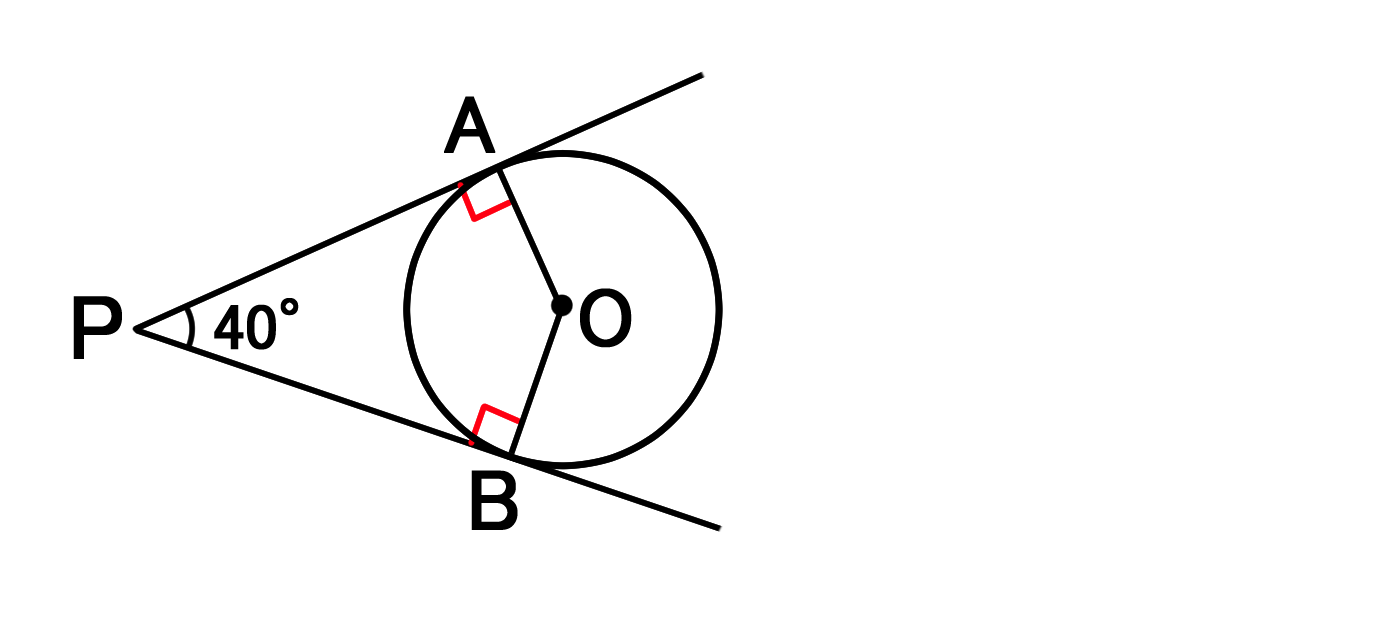



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学




円と角度06 接弦定理 Youtube




円外の点から引いた接線 おいしい数学
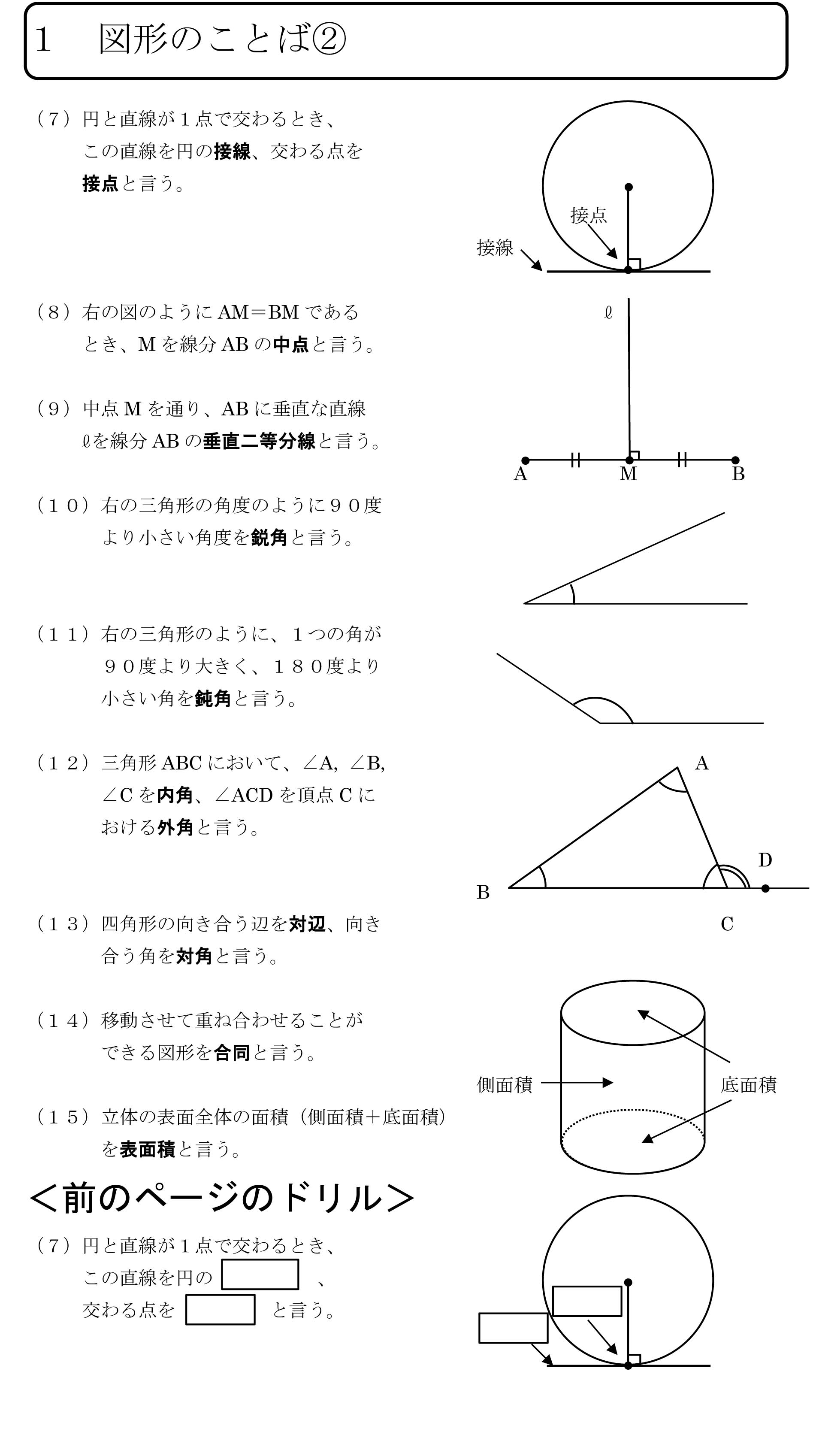



数学図形基本の基本の概要 グローアップ エックス
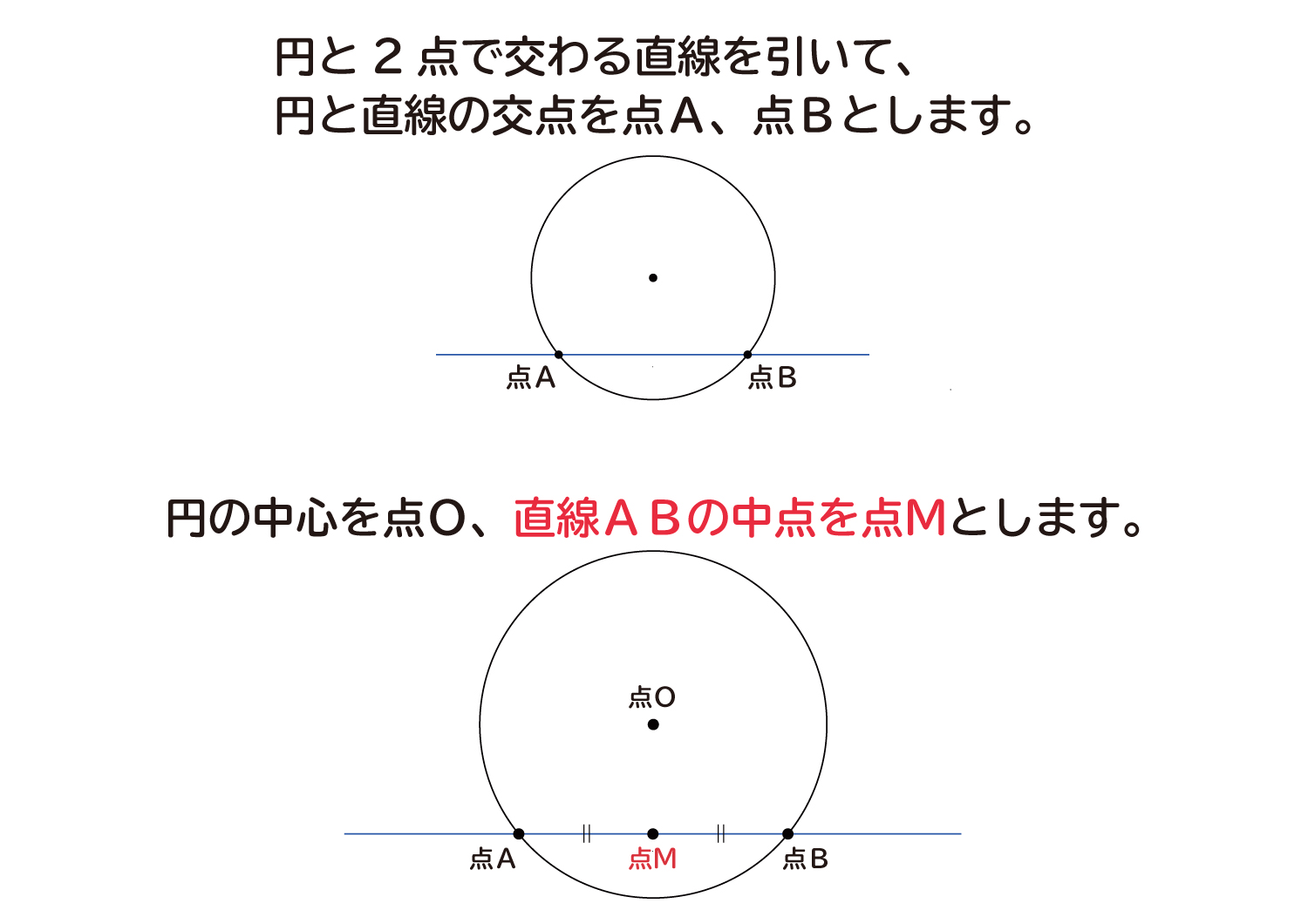



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル
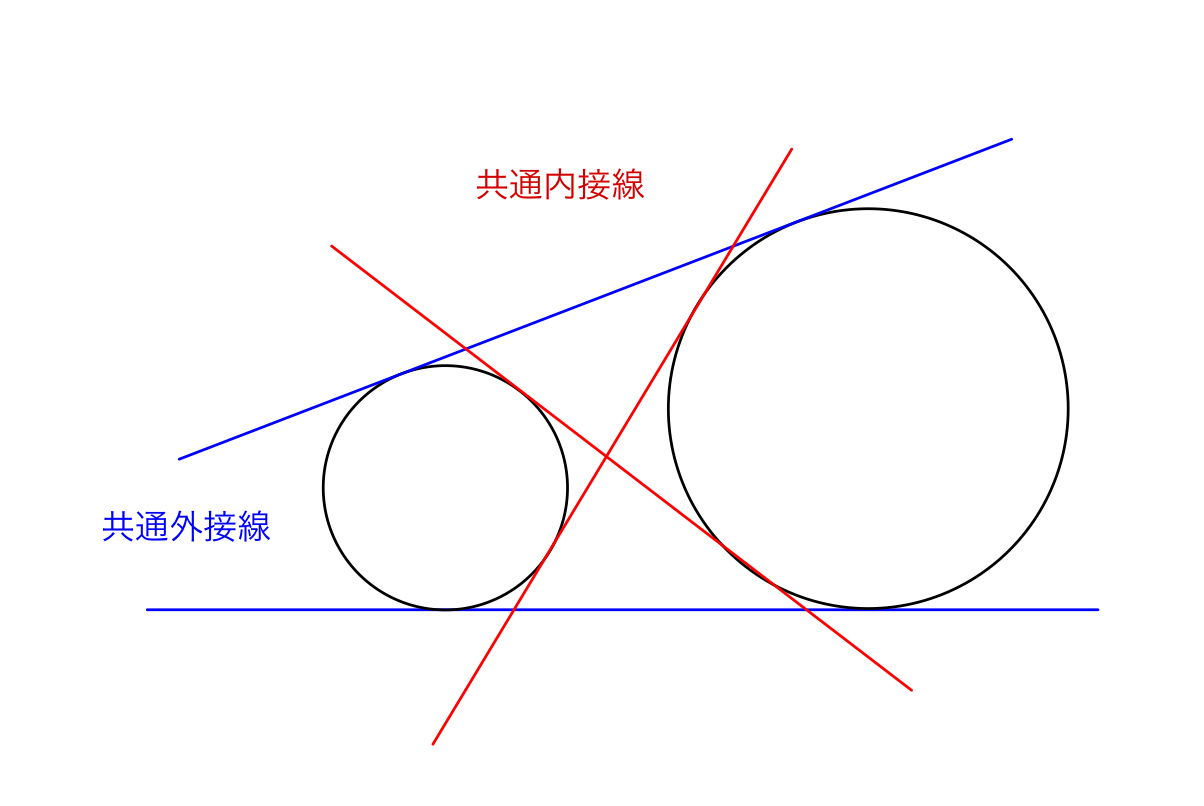



共通接線の問題5パターンの解き方を例題付きで解説 東大医学部生の相談室
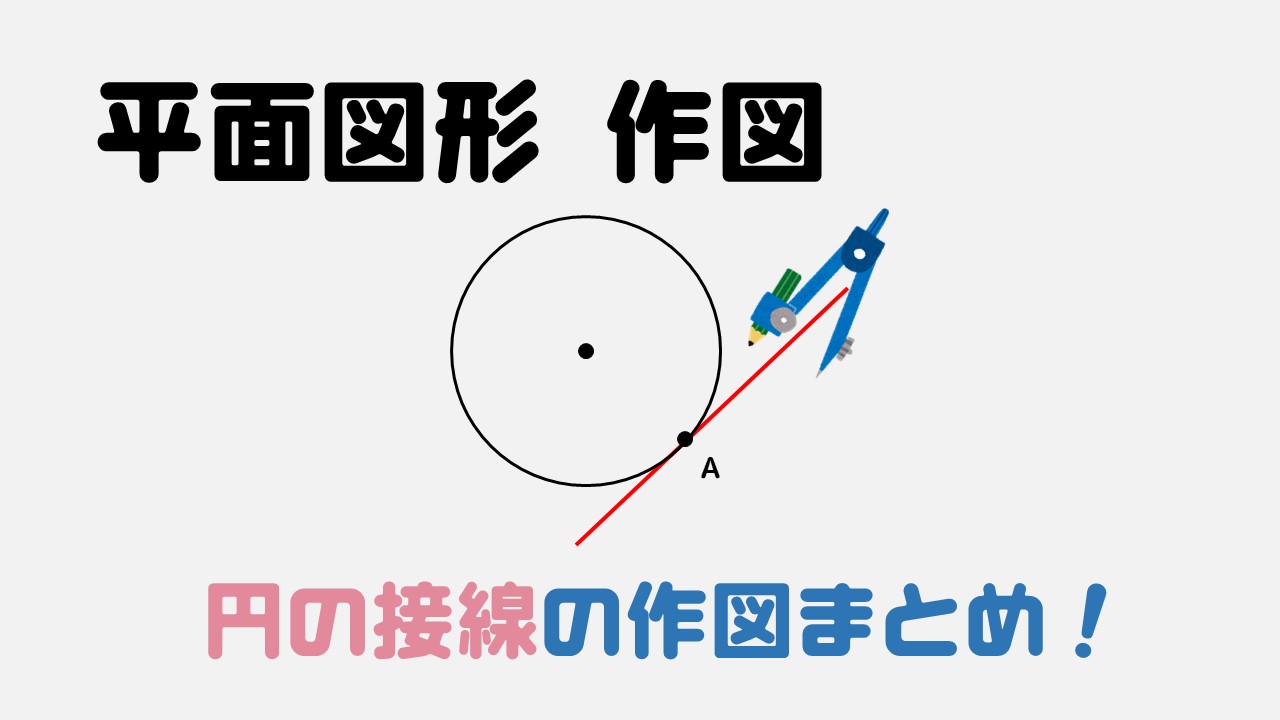



円の接線作図 基本作図から2つの円の共通接線まで解説 数スタ
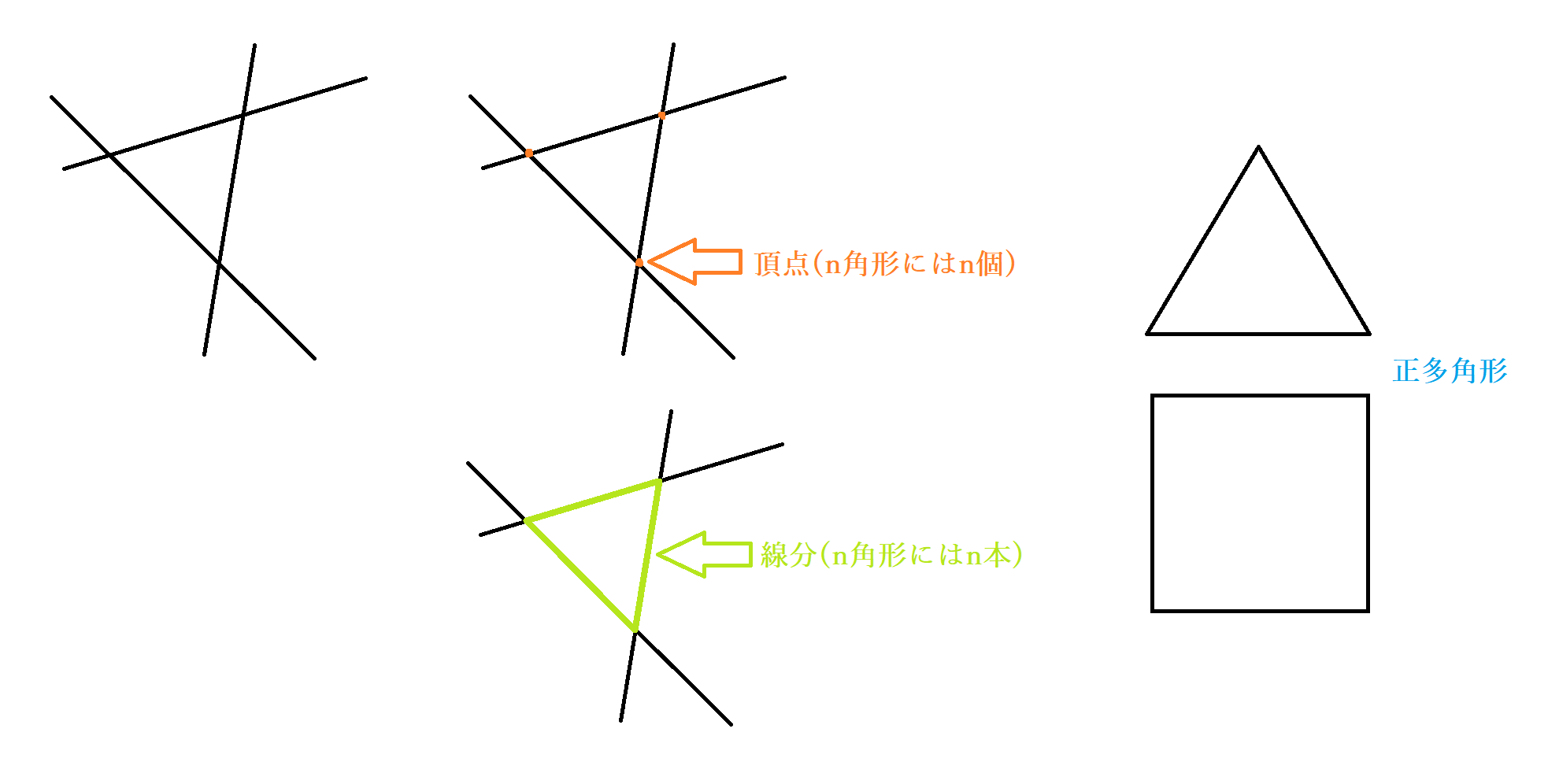



数学 三角形の内心とは 角の二等分線の作図を踏まえた内接円の書き方と証明 Curlpingの幸せblog




07 号 摩擦伝動装置 Astamuse




楕円に正確な接線を引く方法 005 すみながめ Inkscape の使い方を解説




12 号 角度検出装置およびその偏心量推定方法 Astamuse




問2 の 2 だけがわかりません 分かる方お願いします Clear




円外の点から引いた接線 おいしい数学




なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




応用編 第1回東大オープン 軌跡と領域 文系第1問 検算のススメ



図形プログラミングの基礎 マウスでcanvas上の円弧をクリック検出 Satoh
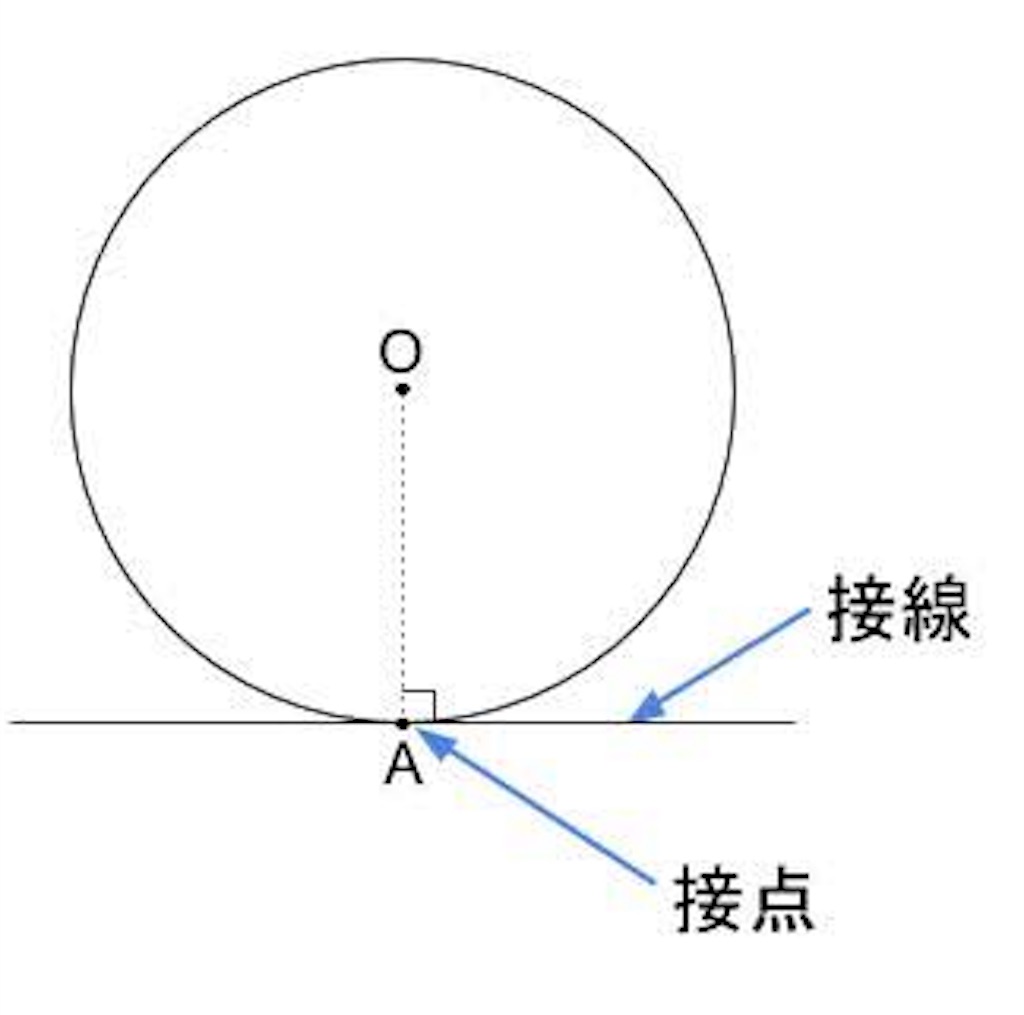



知ってると得 円の接線の作図 円に接する円の作図方法 はてなラボ




中3数学 円の性質と証明 練習編 映像授業のtry It トライイット




数学 中3 56 円周角の定理 基本編 Youtube




特定の問題についての質問ではないのですが Clear




高校数学の平面図形の問題 角度を求める 大分考えましたが できませんで Okwave




数学 円 32 接線と弦の作る角 接弦定理 解説 練習問題 Youtube




定規だけで双曲線に接線を作図 定規とコンパスだけで双曲線の漸近線を作図 Mathlog
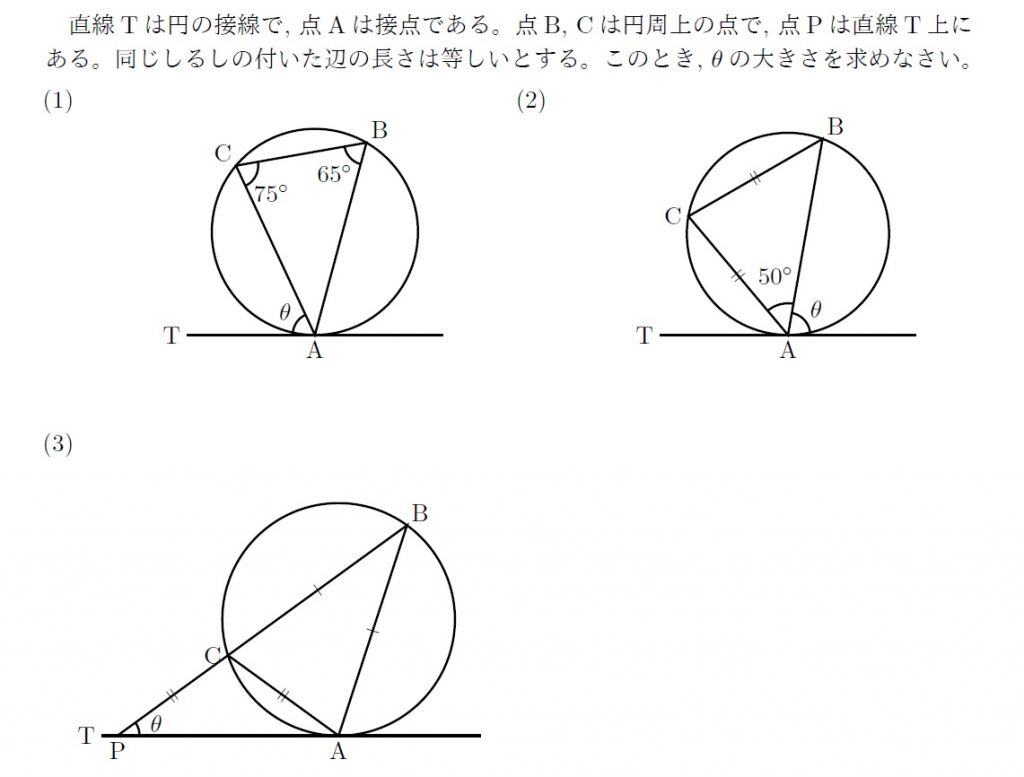



Emathソースコード 円の接線と弦のつくる角度の問題 数樂管理人のブログ
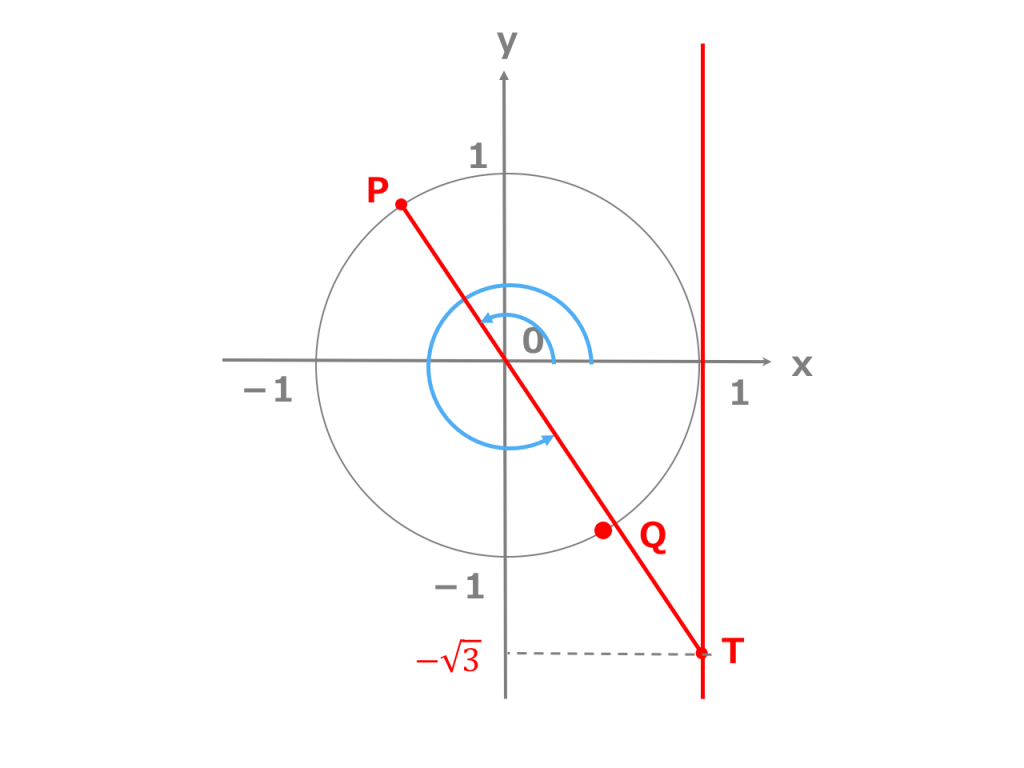



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




中3数学 円周角と中心角 練習編 映像授業のtry It トライイット




中学数学 円と接線 Youtube




接線と弦の作る角を教えてください この画像の問題の解き方 やり方を教えて Okwave



図形プログラミングの基礎 マウスでcanvas上の円弧をクリック検出 Satoh




円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
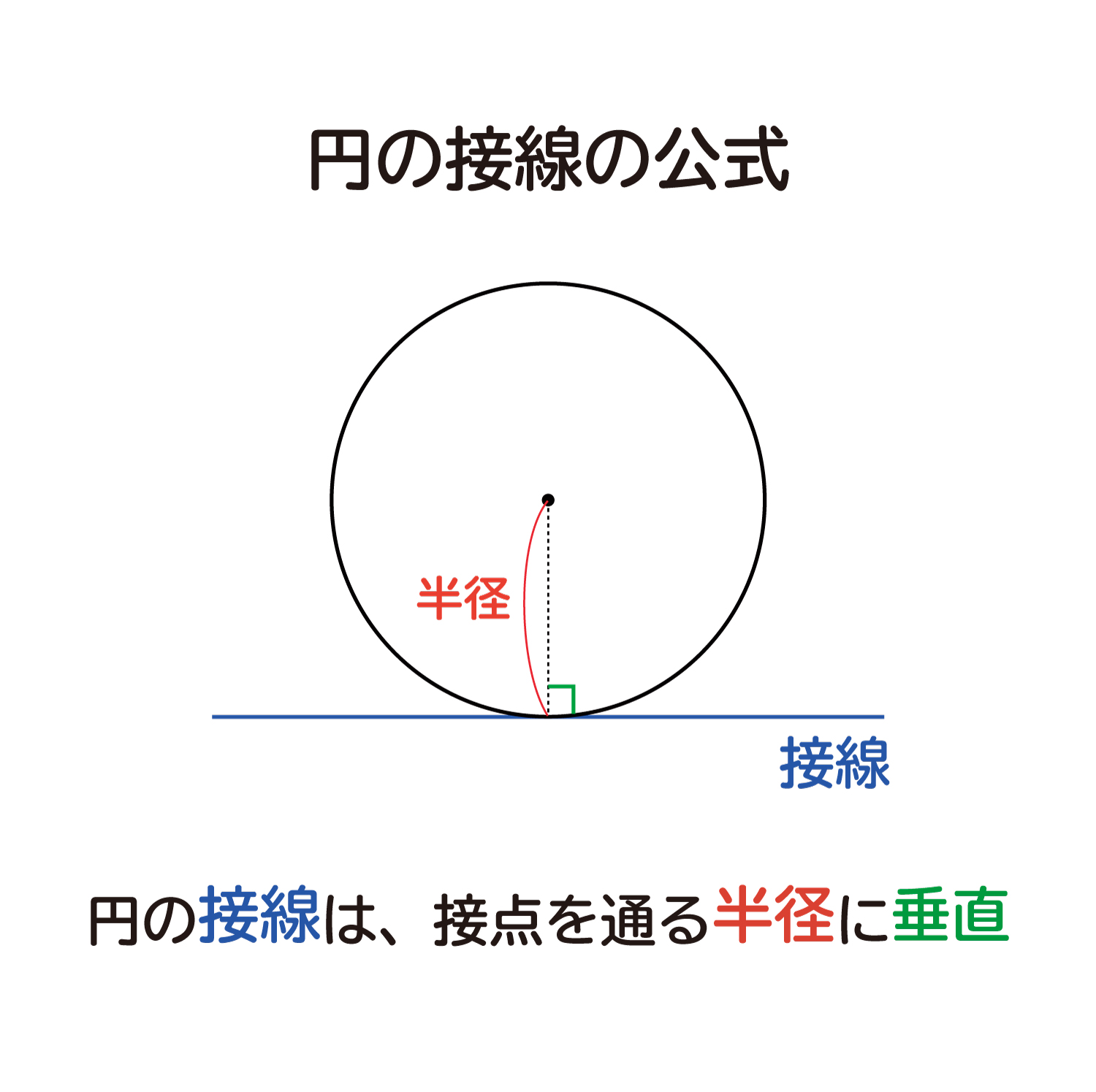



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




円外の点から引いた接線 おいしい数学




円の中心を求める 3つの方法 Wikihow




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
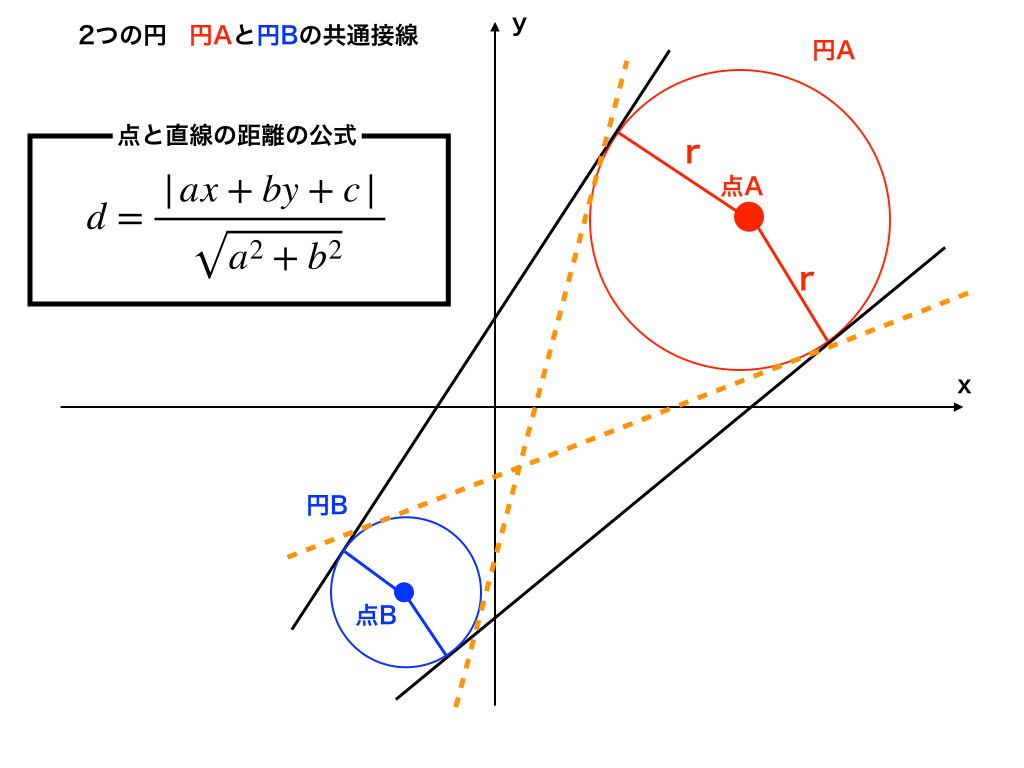



2つの円の位置関係と共通接線の求め方 図形と方程式 2
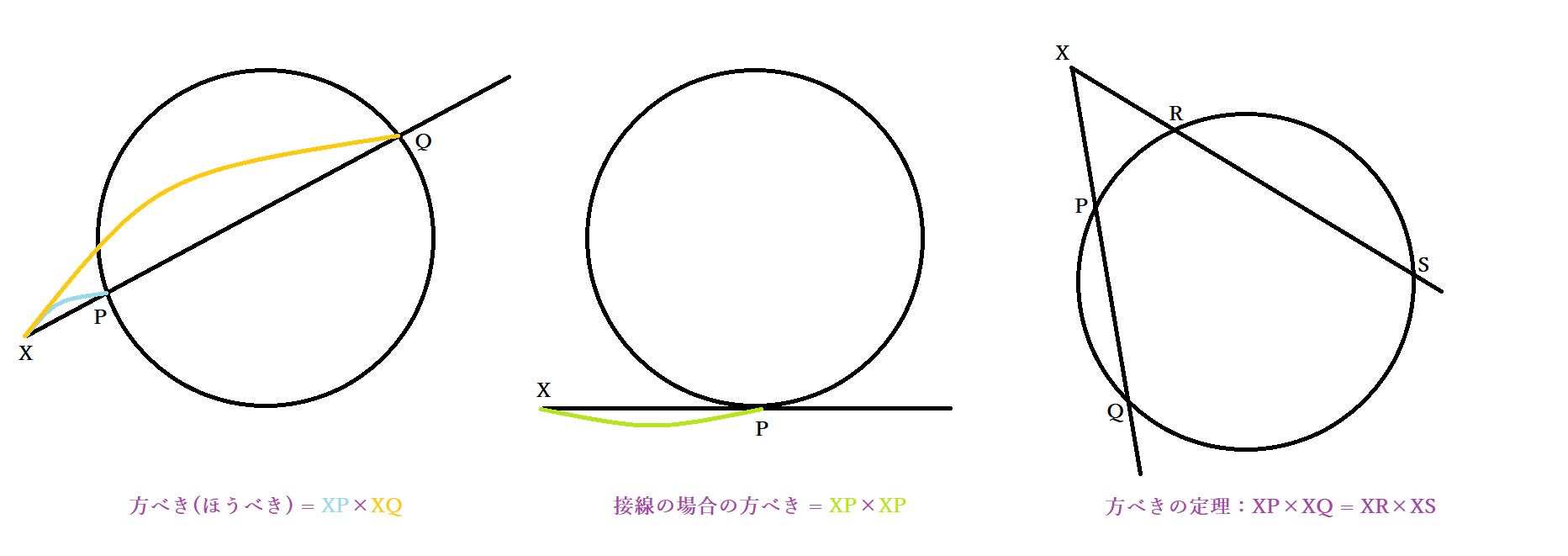



ほうべきの定理とは 方べきの定理の公式を角度や比で証明 中学での問題も Curlpingの幸せblog




円と直線図形01 円と2本の接線 Youtube




数学a 角度の求め方が分かりません 下の図で Atは円oの接線 Aは接点 Okwave



H28測量士試験過去問題解説 第10回 午前no 25 Geo Solutions 技術情報
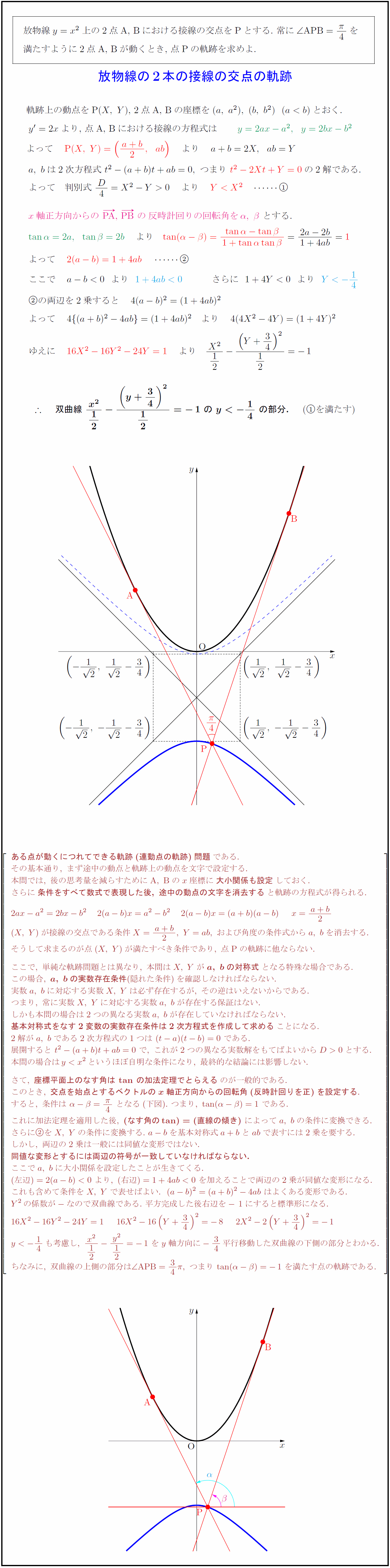



高校数学 放物線の2本の接線 なす角45 の交点の軌跡 受験の月




円 接線 角度 円 接線 角度 中学 Trangjpsip




円周角と円の外の点を結んで おときち副塾長 電脳空間学習塾かもん Youtube



作図 三角形の内接円 外接円のかき方をポイント解説 数スタ
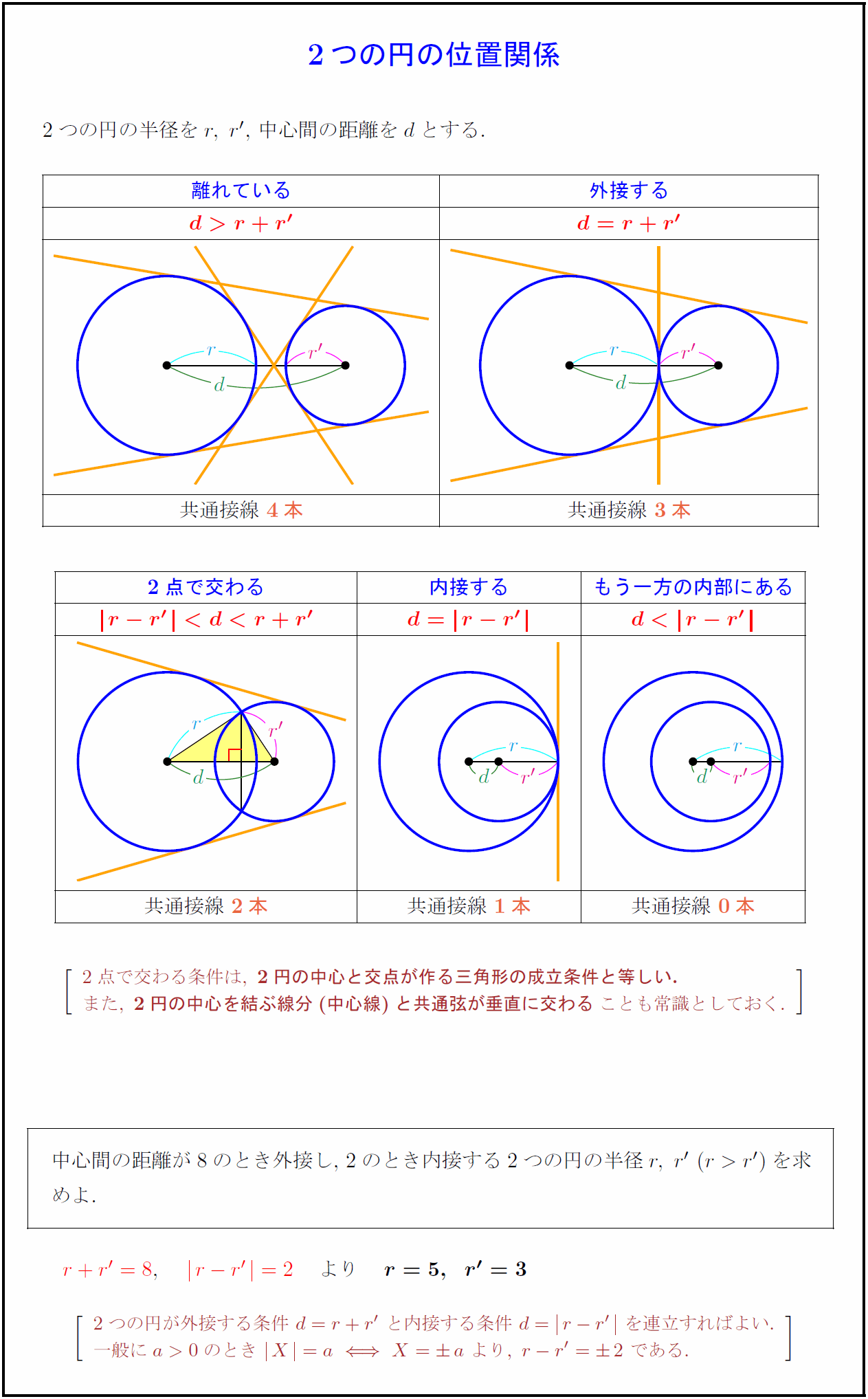



高校数学a 2つの円の位置関係5パターン 受験の月



方べきの定理とは 証明や定理の逆 応用問題をわかりやすく解説 受験辞典




ヒント1 勾配接線の求め方 数学 21




号 グリーンタイヤの製造装置及びグリーンタイヤの製造方法 Astamuse




円外の点から引いた接線 おいしい数学
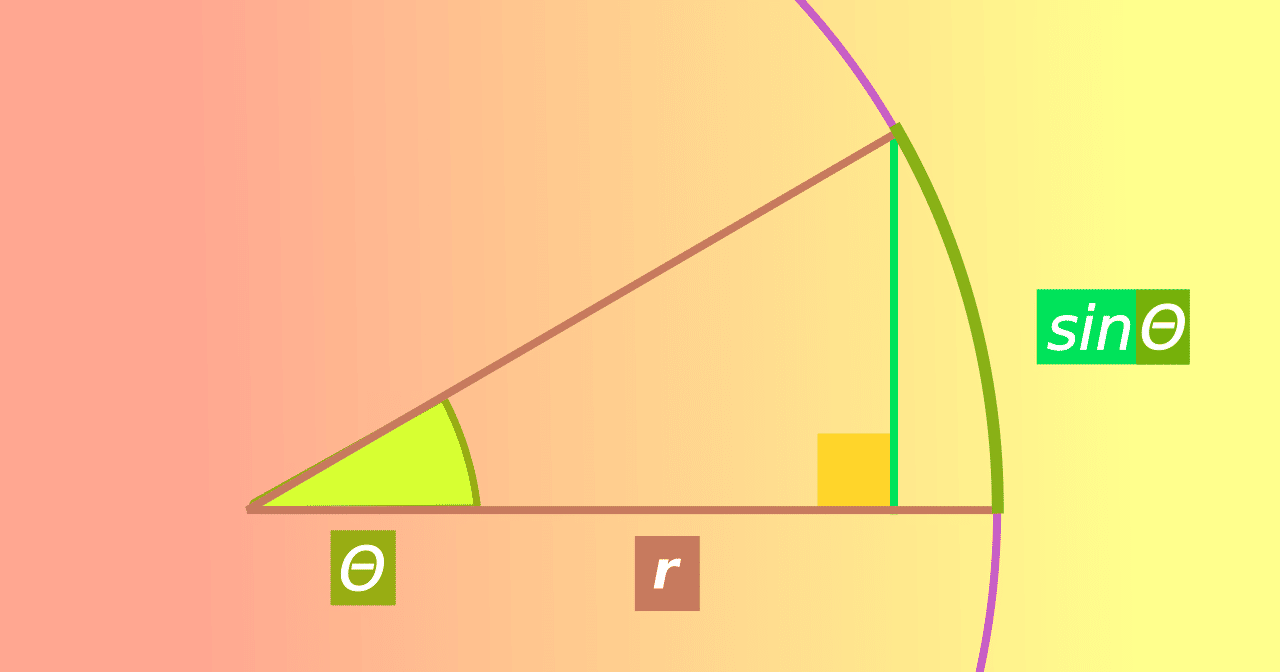



角度がとても小さいとき Sin8 は 8 に近似できる Rijk Note




教えて頂きたいです 答えは65です Clear




円と直線 切り取る線分の長さ 弦の長さ を求める問題を解説 数スタ




いろいろな作図 さわってうごく数学 Aquaアクア Para Android Apk Baixar




教えてください Clear
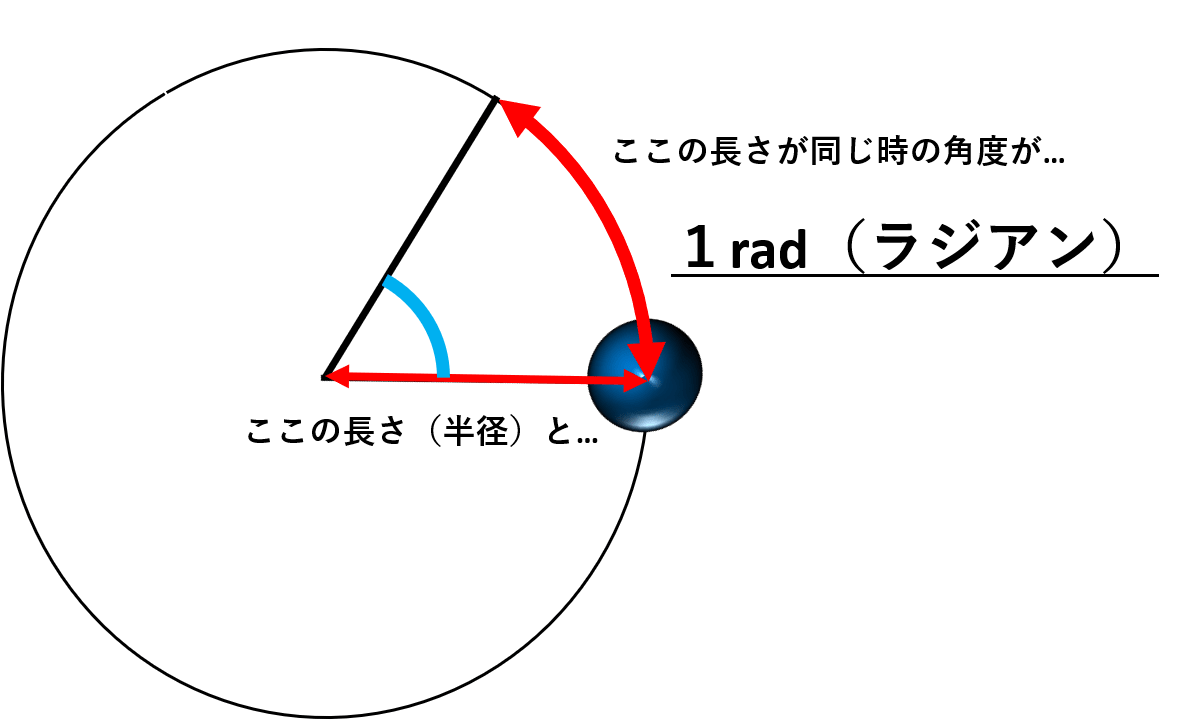



角運動の並進速度 接線加速度 求心 向心 加速度の求め方 陸上競技の理論と実践 Sprint Conditioning




作図 角度15 30 45 60 75 90 105 の作り方を解説 数スタ
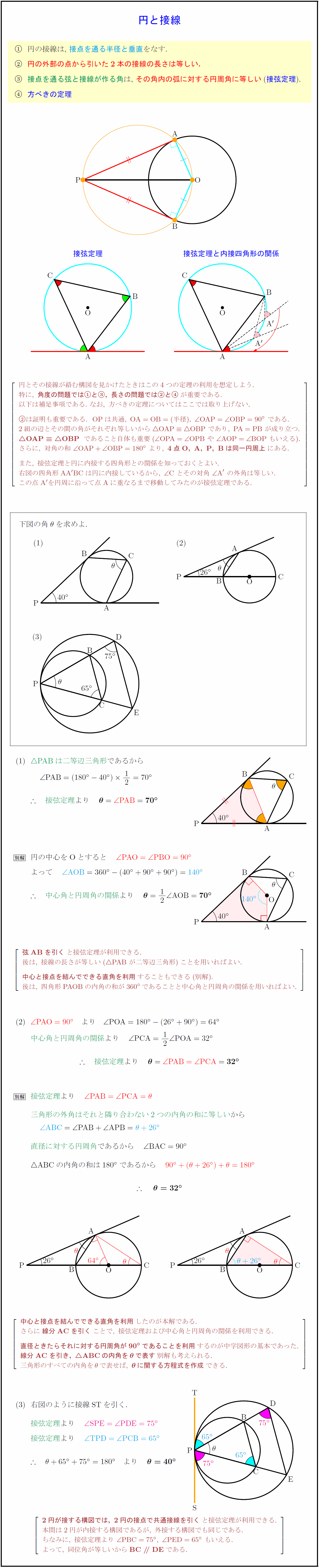



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月




ぬるいパースが描けるようになりたい 円柱の描き方4 接平面と接線




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ
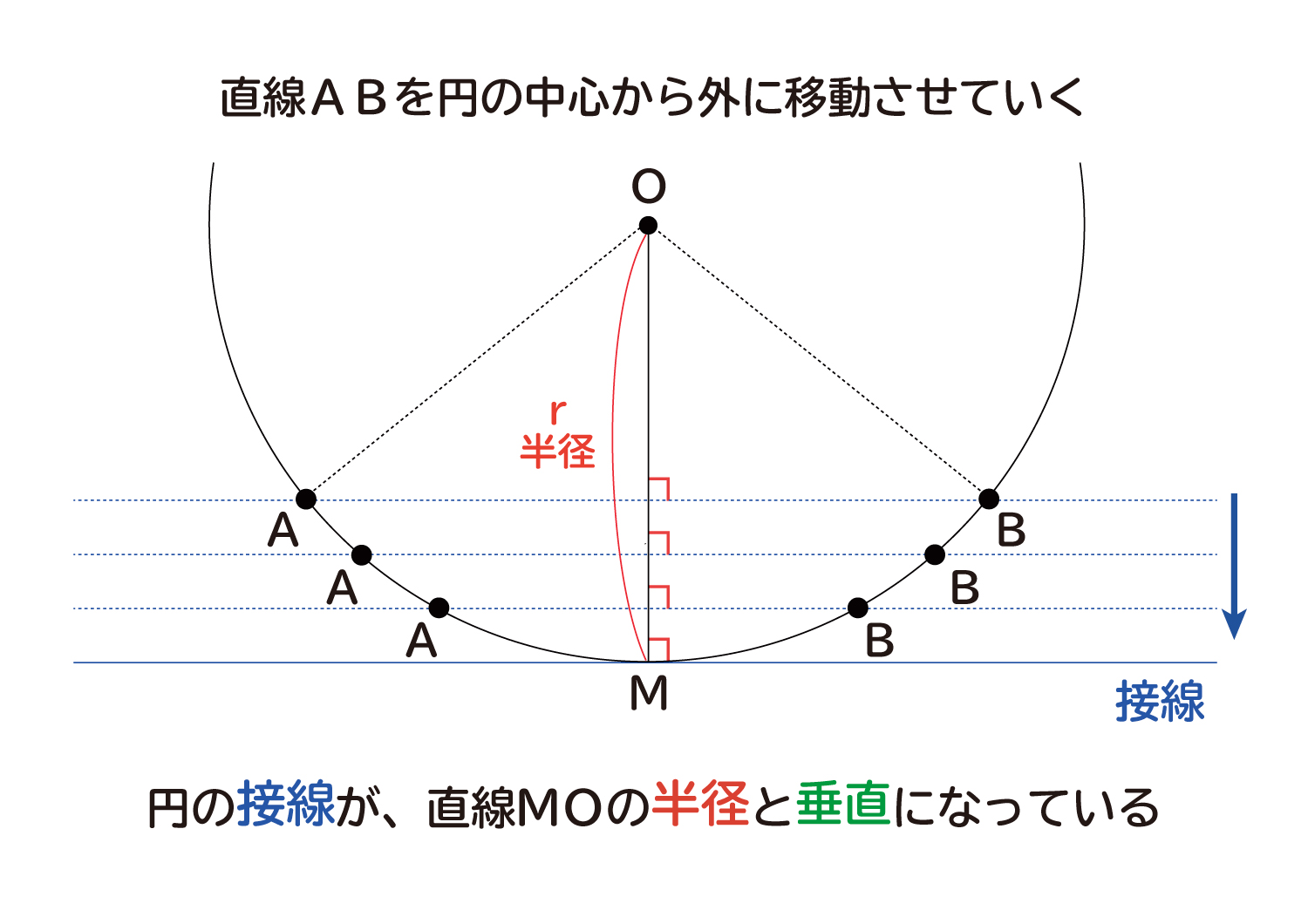



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




17 号 水道メーター Astamuse
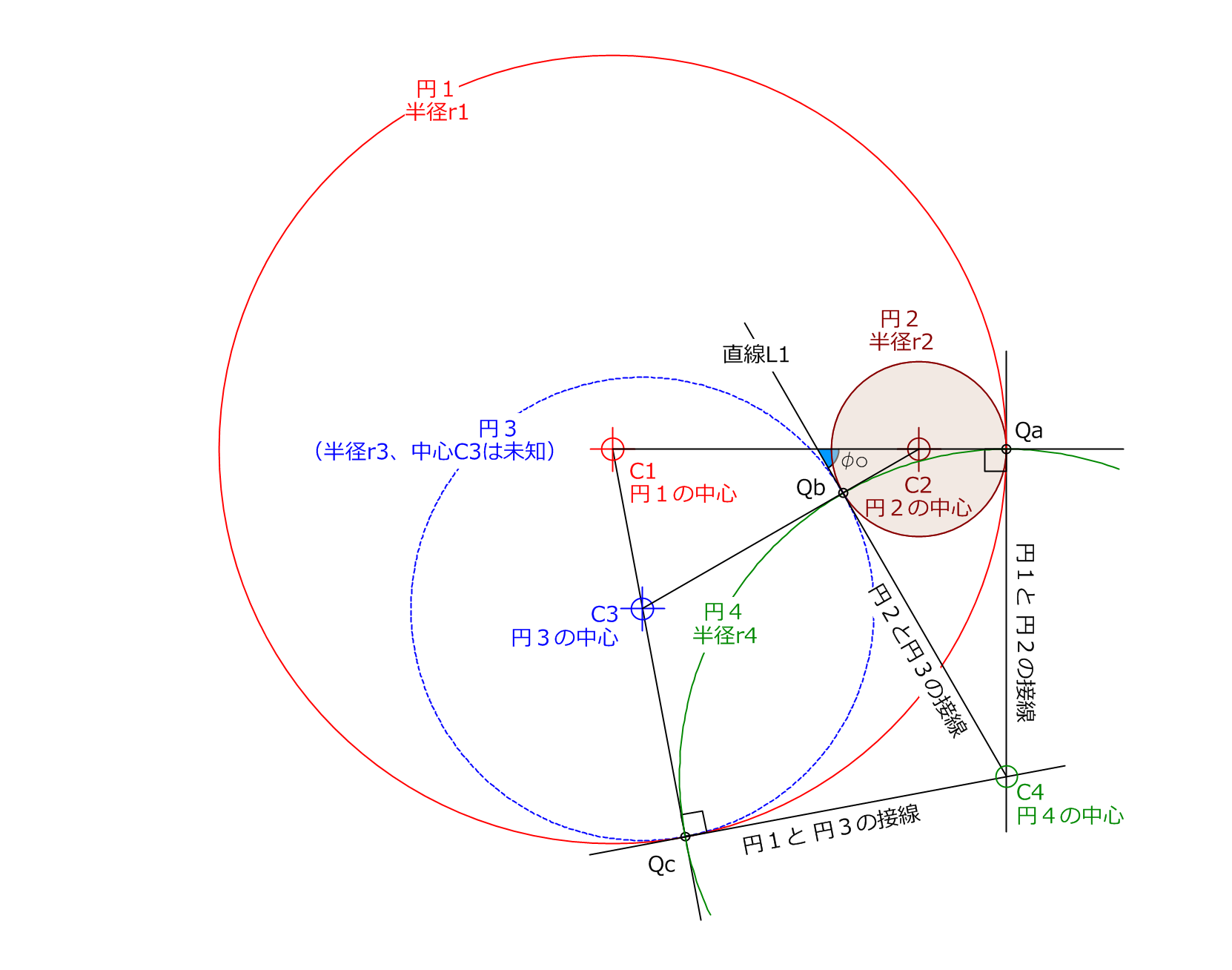



弧状ブレードの場合の球送り 1 ただのつぶやき



3分でわかる 接弦定理の証明 使い方のコツ 合格サプリ




円と接線 教遊者




高校数学a 2つの円の共通外接線と共通内接線の長さ 受験の月




トロコイド曲線の接線 ライブラリ Opeo 折川技術士事務所




公務員の数的処理の問題でわからないので教えてくださ Okwave




中3数学 円周角の定理の逆 練習編 映像授業のtry It トライイット




問3で なぜこの解答のように点cの弧の接線の方向に重りは運動するのですか Clear
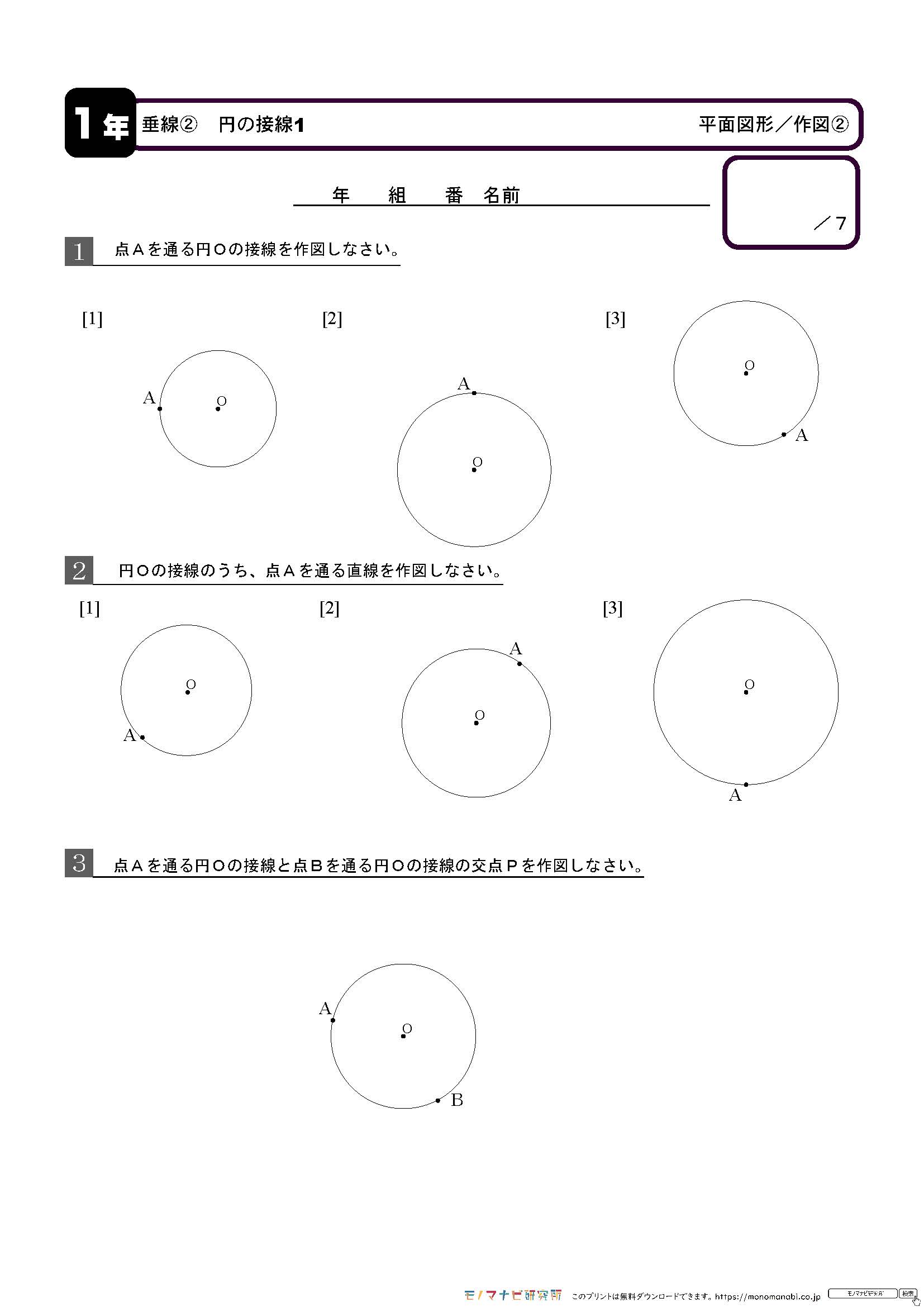



モノマナビ研究所




円の接線の問題です 教えてください Clear




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




接線角度の意味 用法を知る Astamuse
コメント
コメントを投稿